Lee Jaewon

7 minute read

‘Coordinated Multi-Robot Exploration’ 논문 리뷰 포스팅입니다.

공부하며 정리하는 포스팅이기 때문에 다소 직역과 번역에 가까워 질 수 있습니다.

()에 담는 내용은 본인의 부연 설명입니다.

0. Reference

W. Burgard, M. Moors, C. Stachniss and F. E. Schneider, “Coordinated multi-robot exploration,” in IEEE Transactions on Robotics, vol. 21, no. 3, pp. 376-386, June 2005, doi: 10.1109/TRO.2004.839232.

1. Introduction

2. Coordinating a Team of Robots During Exploration

A. Costs

현재 frontier cell들에 이르기 위한 cost를 결정하기 위해서는
동적 프로그래밍 중 하나인 $value$ $interation$을 통해 현재 position에서 모든 frontier cell들까지의 최적 경로를 계산해야 한다.

tuple $(x,y)$는 2차원 occupancy grid map에서 x축의 $x$번째, y축의 $y$번째 cell을 뜻한다.

grid cell $(x,y)$로 가는 비용은 Occupancy value $P(occ_{xy})$에 비례한다.

minimum-cost path는 아래 두 단계를 통해 계산된다.

  1. Initialization. The grid cell that contains the robot location is initialized with 0, all others with $\infty$

    \(V_{x,y} \leftarrow \begin{cases} 0, & \mbox{if }\mbox{$(x,y)\; is\; the\; robot\; position$} \\ \infty, & \mbox{}\mbox{otherwise} \end{cases}\)

  2. Update loop. For all grid cells $(x,y)$ do:

    $ V_{x,y} \leftarrow min(V_{x+\Delta x,\; y+\Delta y} + \sqrt{\Delta x^2 + \Delta y^2}*P(occ_{x+\Delta x,\; y+\Delta y}) $
    $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; | \Delta x,\;\Delta y \in (-1,0,1) \wedge P(occ_{x+\Delta x,\; y+\Delta y}) \in [0, occ_{max}])$

$occ_{max}$는 로봇이 갈 수 있는 grid cell의 최대 점유 확률이다.

이 방법은 모든 grid cell의 값을 최적의 이웃의 값과 이 이웃으로 이동하는 비용에 따라 업데이트 한다.

여기서 Cost는 grid cell $(x,y)$가 다른 cell까지의 거리에 대해 점유되는 확률 $P(occ_{x,y})$와 같다.

(위 식을 간단히 해석해보면 현재 위치 $(x,y)$ 주변에서 가장 가까운 거리내에 점유되지 않은 곳을 선정하는 것이라 볼 수 있다.
점유되지 않을수록 P값이 작기 때문에 P값이 작으면서도 거리도 가까운 지점을 선정하기 위한 식이라 볼 수 있다.)

-1은 unknown space, 0은 free space, $occ_{max}$에 가까울 수록 Occupied로 본다.

즉 unknown space일 때는 누적되는 $V_{x,y}$의 값이 감소되며, occupied에서는 값이 커지기에 cost가 증가한다.

알고리즘의 수렴은 cell이 음수가 아니거나 환경이 bounded되면 보장된다.


위 사진은 cost를 통해 target point를 지정한 모습이다.

B. Computing Utilities of Frontier Cells


Frontier cell들의 효용성(Utility)을 추정하는 것은 굉장히 어렵다.
(Utility? -> 쓸모있는 것, 효용성, 로봇이 쓰기 좋은 정보?)

실제로 특정 위치로 이동해 수집할 수 있는 실제 정보는 해당 지역의 구조에 의존하기에 예측이 불가능하다.
하지만 이미 특정 frontier cell로 이동하는 로봇이 있는 경우, 다른 로봇한테는 그 cell의 효용성이 낮아질거라 예상할 수 있을 것이다.
(이미 로봇이 간 cell로 갈 이유가 없기에 다른 로봇한테는 효용성이 떨어진다.)

그러나 지정된 목표 위치로만 효용성이 줄어드는 것은 아니다.

로봇의 센서는 일반적으로 로봇이 도착하자마자 특정 영역을 커버하기 때문에 로봇의 목표 지점 근처에 있는 Frontier cell의 기대 효용성(Expected Utility)또한 줄어든다.
(로봇의 센서가 목표 지점만 비추는 것이 아니라 그 영역 부근 전체를 인식하기에 목표 지점 근처 cell들의 활용도가 떨어짐. 목표 지점이 있는데 다른 지점으로 갈 이유가 없기 때문에.)

2-B. 에서는 다른 로봇에 할당된 cell들의 거리(distance)와 가시성(visibility)을 기반으로 frontier cell의 Expected Utility를 추정하는 기술을 제시한다.

처음에 각 frontier cell $t$가 환경에서 특정 위치의 유용성에 대한 추가 정보가 없을 때, 모든 frontier cell에 대해 동일한 Utility $U_t$를 가진다고 가정하자.

어떤 로봇의 target point $t’$이 설정되었을 때, 우리는 $t’$주위의 거리 $d$만큼 인접한 frontier cell들의 utility를 감소시킬 수 있다.
이는 로봇의 센서가 거리 $d$이내의 cell들을 덮을 확률 $P(d)$ 에 따라 결정된다.

또한, 지정된 $t’$부터 거리 $d$에 있는 어떤 cell $t$은 로봇이 $t’$ 도착했을 때, 확률 $P(d)$와 함께 센서에 의해 덮일 것이다.

따라서, 우리는 frontier cell $t_n$의 utility $U(t_{n}|t_{1},…,t_{n-1})$를 계산할 수 있다.
이 $t_{1},…,t_{n-1}$은 이미 robot $1,…,n-1$에 할당되어 있다.

Utility에 대한 식은 다음과 같다.
$ U(t_{n}|t_{1},…,t_{n-1}) = U_{t_{n}} - \sum_{i=1}^{n-1} P(\Vert{t_{n}-t_{i}\Vert}) $ … (1)

$t_n$의 Utility는 나머지 Frontier Cell들의 영향을 받아 결정된다.

식 (1)에 따르면, 다른 로봇들이 $t_n$이 보일 수 있는 위치로 이동하는 횟수가 많을수록 $P(d)$가 점점 커지므로, $U(t_n)$ 즉, $t_n$의 Utility는 감소한다.

만약 $t$와 $t’$사이에 장애물이 있다면, $P(\Vert{t-t’\Vert})$ 는 줄어들거나 0으로 설정할 수 있다.

광범위한 실험에서는 $P(d)$가 어떤 환경에서 학습되었는지가 유의미한 차이를 보이지 않으므로, $P(d)$는 다음과 같이 근사할 수 있다.

\[P(d) = \begin{cases} 1.0- \frac{d}{max\underline{}range}, & \mbox{if }d\mbox{ < $max\underline{}range$} \\ 0, & \mbox{}\mbox{otherwise} \end{cases}\]

C. Target Point Selection

각각의 로봇에 적절한 목표 지점(Target Points)을 계산하기 위해서는 각각의 로봇의 위치로 이동할 때의 Cost와 그 위치의 Utility를 고려해야 한다.

특히, 각각의 로봇 $i$는 location $t$로의 cost ${V_{t}}^i$와 $t$의 Utility $U_t$의 균형을 맞춰야 한다.

반복적인 계산을 통해 모든 로봇의 target point를 추정한다.
tuple $(i,t)$를 계산해야 하며, $i$는 로봇의 인덱스, $t$는 frontier cell이다.

Coordinated Multi-Robot Exploration의 Goal 지정 Algorithm 1.은 다음과 같다.

  1. Determine the set of froniter cells.
    –> frontier cell들의 집합을 결정.
  2. Compute for each robot $i$ the cost ${V_{t}}^i$ for reaching each frontier cell $t$.
    –> 각각의 로봇의 $t$로 도달하기 위한 Cost 계산
  3. Set the utility $U_t$ of all frontier cells to 1.
    –> 모든 froniter cell들의 utility를 1로 설정
  4. while there is one robot left without a target point do –>
  5. Determine a robot $i$ and a frontier cell $t$ which satisfy:
    $(i,t)$ = ${argmax_{i’,t’}}(U_{t’}-{\beta} * {V_{t’}}^{i’})$
    –> $(U_{t’}-{\beta} * {V_{t’}}^{i’})$가 최대인 $(i’,t’)$
    즉, Utility는 크면서 Cost는 작은 $(i’,t’)$를 찾아야 함.
  6. Reduce the utility of each target point $t’$ in the visibility
    area according to $U_{t’}\leftarrow U_{t’}-P(\Vert{t-t’\Vert})$
    –> 보이는 목표 지점 $t’$의 Utility 줄이기 (P가 증가하기 때문에)
  7. end while



Algorithm 1.의 시간 복잡도는 $O(n^2T)$이며, n은 로봇의 개수, T는 frontier cell들의 개수이다.

$\beta$는 cost에 대한 Utility의 중요도이다.
$\beta$가 너무 크거나 너무 작으면, 적절한 $(i,t)$를 찾는데 시간이 오래걸려 전체적으로 탐사 시간이 증가한다.

그래서 본 논문에서는 $\beta$를 1로 지정한다.

지금까지의 coordination technique을 적용한 모습은 다음과 같으며,


uncoordinated robot에 대한 모습은 다음과 같다.


coordinated robot은 각기 다른 next explortion target을 지정한다.

탐사 중에 coordinating team of robots에서의 한 가지 질문점은 언제 target location을 재계산할 것이냐에 관한 것이다.
제한(Unlimited)이 없는 통신 상황에서는 로봇이 지정된 target location에 도달했을 때 혹은 계산 후 경과한 시간이 임계치를 초과할 때 새로운 목표 지점을 계산하는 것이다.

D. Coordination With Limited Communication Range

실질적으로, 로봇들이 어느 시점에서나 정보를 교환할 수 있다고 가정할 수 없다.

무선 통신과 같이 제한된 통신 범위에서는 로봇이 특정 시점에 다른 로봇과 통신을 못할 수도 있다.

로봇간의 거리가 너무 커져 모든 로봇이 통신할 수 없는 경우에는 Centralized Approach를 적용할 수 없다.

이 논문에서는 제한된 통신 범위에 대해서 그들끼리 통신 가능한 sub-team을 적용하여 접근한다.

이 때, 최악의 경우에도 로봇은 각각의 Exploration을 진행하는 상황으로 이어진다.

제한된 통신의 경우, 통신이 끊기면 다른 로봇의 목표를 알 수 없기 때문에 중복된 작업을 초래할 수 있다.
이 논문의 전략은 각 로봇이 다른 로봇에 할당된 최신 목표 위치를 저장하면 통신 범위가 초과되어도 로봇이 이미 탐색한 장소로 이동하는 것을 피하기 때문에 전반적인 성능이 향상된다.

이 전략은 소규모 로봇 팀의 맥락에서 유용하다는 것이 밝혀졌다.

3. Collaborative Mapping With Teams of Mobile Robots

주어진 환경을 탐사하고 그들의 행동을 coordinate하기 위해 로봇은 환경에 대한 자세한 맵(detailed map)이 필요하다.

그리고 로봇은 맵을 온라인으로 그려야 한다. 탐사 작업에서 온라인 특성은 굉장히 중요하다. mapping은 지속적으로 어디로 갈지 결정을 해야하기 때문이다.

환경을 매핑하려면 로봇은 두가지 타입의 센서 노이즈에 대해 대응해야한다.
하나는 인식(Perception)에 대한 noise와 다른 하나는 Odometry에 대한 noise이다.

mapping에 대한 문제로 인해 Localization에 내재적인 문제가 생길 수 있다. 이는 로봇의 위치 결정 문제를 의미한다.

mobile robot mapping problem은 CML(Concurrent mapping and localization problem)이나 SLAM에서도 종종 일어난다.

이 논문의 시스템에서는 로봇이 환경을 탐사하는 동안 일관된 지도를 계산하기 위해 통계 프레임워크를 적용한다.

각 로봇은 빈 grid map으로 시작하며, 탐색 중에 두 가지 작업을 동시에 수행한다.
이는 자신의 위치에 대한 maximum likelihood estimate와 map에 대한 maximum likelihood estimate를 결정한다.

가능한 localization error를 복구하기 위해, 각 로봇은 ‘true’ location을 특징짓는 Posterior density을 유지한다.

이 논문에서는 두 가지 가정에 의존한다.

  1. 로봇은 스캔 범위가 상당히 겹치도록 가까운 위치에서 작동을 시작해야 한다.
  2. 소프트웨어에게 로봇의 대략적인 상대 초기 자세를 알려주어야 한다. 이 때 50cm, 20도 방향의 오차가 허용된다.

좌표화를 달성하기 위해서, team은 각각의 로봇의 지도를 전달할 수 있어야한다.

현재 시스템에서는 cluster를 형성하는 ad hoc network를 설정하는 것으로 가정한다.
(ad hoc network란 핸드폰처럼 기지국과 단말이 통신하는 형태가 아니라, 각 단말끼리 연결이 되는 형태이다.)

로봇이 보낸 메시지는 해당 cluster내의 모든 로봇에게 전달되야한다. 두 개의 클러스터가 병합될 때마다 로봇이 환경 상태에 지나치게 confident하지 않도록 주의해야한다.

각 cluster가 해당 cluster에 의해 만들어진 모든 관측으로부터 구축된 occupancy grid map을 유지한다고 가정하자.
예를 들어, 지도 ‘m’을 공유하는 두 로봇이 통신 범위를 벗어나고, 그들이 개별 탐색을 하면 그들의 지도를 업데이트 하며 ‘m1’, ‘m2’ 두 개의 다른 지도를 얻는다.

이제 다시 로봇이 통신하고 지도를 교환할 수 있다고 했을 때, recursive update rule을 통해 ‘m1’, ‘m2’를 결합하는 경우
원래 ‘m’에 포함된 정보가 결과 맵에 두 번 통합되므로 허용되지 않는다.

센서 정보의 다중 사용을 방지하는 몇 가지 방법이 있다.
한 가지 해결책은 위에서 언급한 것처럼 로봇이 정보를 두 번 이상 교환하는 것을 방지하는 것이다.
하지만 이는 다중 로봇 시스템의 이점을 감소시킨다.

대안은 각 로봇이 서로에 대해 개별적은 맵을 유지하는 것이다.
공동 지도에 결합할 수 있는 이 지도들은 별도로 업데이트 될 수 있다.

이 접근 방식에서 각 로봇은 로봇에 의해 인식된 센서 측정의 로그를 서로에 대해 저장한다.

또한, 로봇은 다른 모든 로봇에 전송된 최신 측정 타임스탬프를 포함하는 작은 데이터 구조를 유지한다.
이것은 다른 모든 로봇에 의해 수신된 측정값을 폐기할 수 있다.

4. Experiment Result

Test

  • Without Coordination


  • With Coordination (Perform better)


각각의 로봇이 같은 지점으로 향하지 않고, 다른 지점을 탐사.
복도의 Utility가 감소.

Simulation

Unstructured, Office, Corridor에서 수치적 평가를 위해 Simulation 진행.




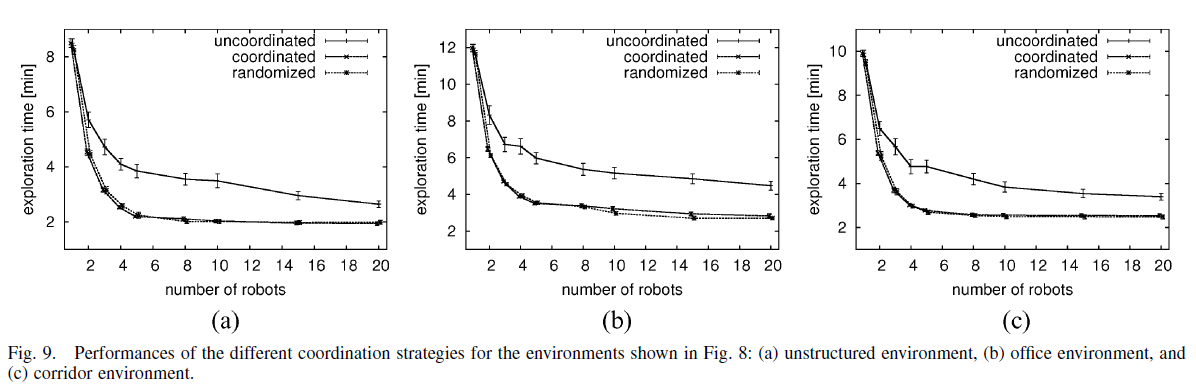
Uncoordinated에 비해 탐사 시간 감소, 하지만 randomized 방식과 큰 차이 X


계산 시간은 Uncoordinated에 비해 더 걸리지만, randomized 방식보다 더 적은 계산 시간을 보임.
–> 전체적인 성능이 좋다.

📣
포스팅에 대한 오류나 궁금한 점은 Comments를 작성해주시면, 많은 도움이 됩니다.💡

Leave a comment

You may also enjoy