Rapidly exploring Random Tree Star (RRT*)

RRT* Path Planning 기법에 관한 포스팅입니다.

Rapidly exploring Random Tree STAR (RRT*)

개요

RRT*(RRT star)는 Sampling-Based Algorithm 중 하나이다.

RRT는 Karamann가 제안했으며, 충분하게 많은 수의 샘플점을 발생시킨다면 최적해로 수렴된다는 것이 증명되었다.

RRT는 고차원 최적 경로 계획 문제를 해결하는데 큰 전환점이 되었으며 실제로 많은 문제에 적용되어 그 효용성이 입증되었다.

RRT의 변형버전은 사실상 RRT의 변형버전일 만큼 학계에서도 많은 관심을 불러와
최근 수년간 RRT에 관련된 논문의 숫자가 폭발적인 증가를 보이고 있다.

최적해 수렴 특징뿐만 아니라 샘플링과 트리를 이용하는 자료 구조적인 특징으로 인해 경로 탐색의 시간 면에서도 이점을 가진다.

RRT와의 차이점

RRT* 알고리즘은 RRT 알고리즘과 근간은 동일하다. 다만 RRT와 두 가지 차이점이 있다.

RRT와 달리 부모 노드의 재선정이 일어나며, 트리의 재구성이 일어난다.

결국 RRT를 진행하는 것은 동일하지만 일정 반경 내의 주변 노드들 중에서 비용을 줄일 수 있는 기존 노드가 존재한다면 이를 임의의 새로운 노드가 대체하는 방식을 반복적으로 수행하면서 최적의 경로를 찾는다.

이때의 비용(Cost)는 부모 노드(혹은 Vertex)에 대해 이동한 거리이다.

대략적인 순서

• RRT에서는 무작위 샘플링 점들 중 q_new와 가장 가까운 q_near가 부모 노드가 되었지만, RRT*에서는 q_new를 중심으로 일정 반경에 있는 노드를 뽑는다.
  

• 뽑은 노드들 중 q_new와 가장 가까운 q_near와의 비용을 비교하여 가장 적은 비용을 가진 노드를 부모(q1)로 선정한다.

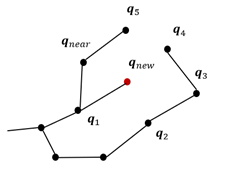
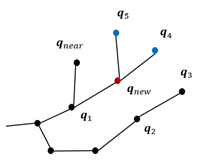
• 두 번째 차이점인 트리의 재구성은 q_new를 중심으로 일정 반경에 있는 노드들의 비용과 그 노드들이 q_new의 자식 노드로 다시 연결됐을 때의 비용을 비교한다.

• q_new의 자식 노드로 연결되는 비용이 더 작다면, 기존 부모 노드와의 연결을 끊고, q_new의 자식 노드로 연결하여 트리를 재구성한다.

장점

• RRT와 비교해 비용을 기준으로 점근적으로 최적에 수렴하도록 하는 것에 의미가 있다.

Reference

• Karaman S, Frazzoli E. Sampling-based algorithms for optimal motion planning. The International Journal of Robotics Research. 2011;30(7):846-894. doi:10.1177/0278364911406761
• https://pasus.tistory.com/77

📣
포스팅에 대한 오류나 궁금한 점은 Comments를 작성해주시면, 많은 도움이 됩니다.💡